С точки зрения математики все получилось гладко и красиво. А вот музыканты были более критичны: некоторые частоты звучат негармонично — их нужно слегка подкорректировать. В те времена ученые были увлечены теорией простых чисел. Считалось, что гармония может быть создана только на основании отношений между простейшими константами. Были исследованы
самые разные варианты. Остановились на пропорции 4:5:6, которая приводила к самому гармоничному звучанию из всех имеющихся сочетаний. Модель звукоряда на основе отношения 4:5:6 оказалась легко реализуемой. Пришлось, правда, отказаться от гармоники 14/8, которая в новый ряд уже не вписывалась. Гармоники 11/8 и 13/8 также пострадали, их пришлось несколько повысить. Итого осталось семь нот (рис. 5.1):

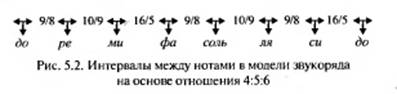
Беглый взгляд на получившийся рисунок показывает, что ряд интервалов получился неравномерный, поскольку характер верхних и нижних стрелок неодинаковый. Еще более очевидным данный факт становится после рассмотрения рис. 5.2, на котором указаны интервалы между соседними нотами:
Если построение октавы каждый раз начинать с новой ноты, то получится семь совершенно разных рядов с различным порядком интервалов внутри. Все октавы оказались наделенными особыми характерами, поэтому в свое прем я им дали персональные имена: обуянный грустью «лидийский»; богатый, торжественный и праздничный «ионийский» (мажор); «миксолидийский»; важный и воинственный «дорийский»; печальный и горестный «эолийский» (минор); вдохновенный и приподнятый «фригийский»; «локрийский». До наших Дней дошли только два из них.
Таким образом получился относительно гармоничный звукоряд. Но несколько проблем так и не нашли своего решения.
Пифагорово решение проблемы транспонирования
При игре ансамблем или при сопровождении солистов возникает необходимость транспонирования мелодии по высоте (от латинского transponere — перекладывать, перемешать). Если чисто механически перенести нотную запись на несколько шагов выше или ниже, то мелодия окажется в совершенно ином строе. Где же выход?